2.2.1  :  Semi-analytic modelling at MPA: L-Galaxies

The merger tree structure of halos extracted from the raw simulaiton results, is used as the skeleton for semi-analytical models (SAMs) of galaxy formation, from which synthetic galaxy catalogues are constructed. Here the SAGF algorithm is described in terms of the actual, file-based, simulation products.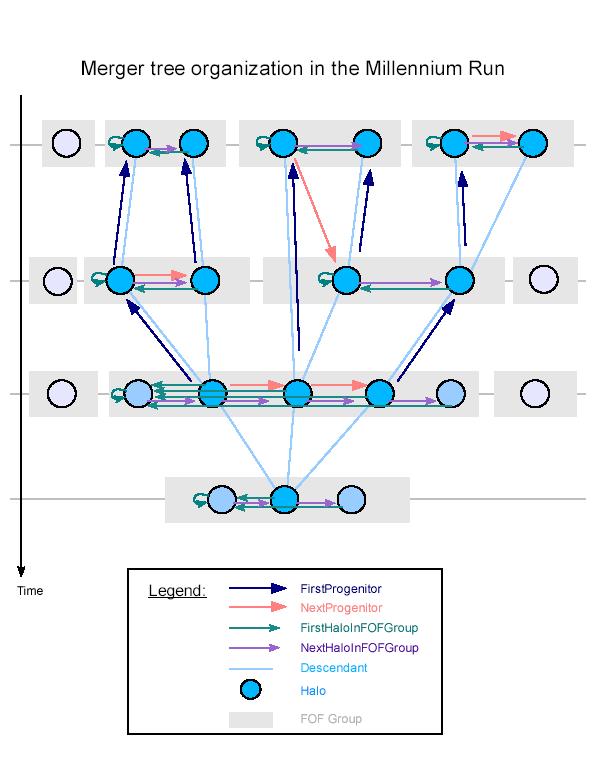
(This description is extracted from private communication from Volker Springel.)

The postprocessing of the Millennium simulation data proceeds in several stages. The first step is the determination of friends-of-friends (FOF) groups, which is done by the simulation code itself. The second step involves running an algorithm that decomposes each FOF group in a set of gravitationally bound (sub)halos and determines physical properties for them. These halos are the actual objects that are then used to construct merging trees.

The merger tree construction itself involves two steps. The first step is a determination of a descendant halo for each halo. The descendant always lies in the future, in >99.9% of the cases in the subsequent output, but in certain situations, an output may also be skipped. The descendant information already uniquely defines the merger tree of the whole simulation. However, in order to simplify further processing, the merger tree is reorganized in a further step such that distinct pieces of the tree (corresponding to merger trees of halos found at the final time) are stored separately, in a form that makes it convenient to walk these trees. These trees also contain all the physical properties of the corresponding halos, such that they form the only input required to run the semi-analytic galaxy formation code on them.

The construction of the galaxies is done by walking the merger tree more or less in a depth-first fashion by calling the function construct_galaxies() recursively. This function forms the backbone of the program. It first constructs the galaxies of all the progentitors of the present halo. These galaxies are then combined (join_galaxies_of_progenitors())and evolved forward in time by the function evolve_galaxies(), such that once the function finishes, we will have obtained the galaxies for the halo that was passed as an argument. All the details of the modelling of the galaxy formation process are contained in the two functions join_galaxies_of_progenitors() and evolve_galaxies(). The walk of the merger tree encapsulated in construct_galaxies() should be pretty generic and essentially independent of any detail of the galaxy formation model itself.

Note again that in all of the above, the word "halo" refers to a generalized concept of `subhalo', i.e. physically a subhalo may represent an embedded substructure within a larger halo, or a `background halo' that hosts substructures itself. When we follow subhalos over time it is not important to know these geometrical differences. All that matters is that each subhalo carries one or several galaxies, and that these galaxies should be associated with the descendant subhalo at the future output. So subhalos can be treated all on the same footing, and its perhaps best to think of them as a generic object, a "halo".

There is however one exception to this. Certain subhalos are given a special meaning, based on a secondary grouping criterion. This grouping makes reference to the two-stage group identification that we do: We first decompose the particle set into FOF groups, and then each FOF group is decomposed into its constituent subhalos. As explained above, the merger trees are built for the total set of subhalos found in this way, without making any reference to the FOF groups. However, in the physical modelling of galaxy formation, we use the FOF information at one place: We assume that only the biggest subhalo in a FOF group receives fresh cool gas dropping out due to radiative cooling.

This basically means that in our merger tree we somehow need to know which halos belong to the same FOF-group, so that we can select the biggest one of them as the "main halo" of the group - this is then the one which will receive the cooling gas.

The above then introduces a complication in the recursive construction of the galaxies. Because the physical model for the cooling rate of gas (needed when the galaxy population of a halo is evolved in time) starts out with an inventory of all the baryons in a given FOF-group, one needs to know the present state of all the galaxies in a given FOF group to compute this... This means that one cannot simply construct the galaxies just based on the merger tree of a given subhalo, because for working out the cooling rates, one may also need information from halos that are only linked to the present tree by a weaker relation of the form that they are part of some of the FOF halos under consideration. One therefore needs to ensure that galaxies of all halos in a given FOF group are already constructed when it comes done to computing the cooling rates.

The above issues are resolved by walking the tree in a slightly more complicated way, and by temporarily storing all the galaxies that have been constructed for a given halo in memory. The recursive walk to construct the galaxies is augmented by the following additional check. After we call construct_galaxies() for all progenitors of a given halo, we check whether all the galaxies have already been constructed for the FOF group. If not, we loop over all the subhalos in the same FOF group and call construct_galaxies() for them if they have not already been processed. That way, we are sure that before join_galaxies_of_progenitors() is called for the present halo, the galaxies for its main halo have already been constructed.